Complexity Abounded
In August, when the physicists at London Centre for Nanotechnology at UCL along with their collaborators at European Synchrotron Radiation Facility in Grenoble, France were studying the properties of high-transition-temperature copper oxide superconductors , observing the way microstructures formed as they cooled down little did they know they were after a miracle. To their astonishment, the oxygen atoms put themselves in well –organized so called fractals, a geometric shape that has recursive properties. Till now, it was assumed that the formation was random instead of following a well-known pattern. Fractals was something they least expected it to be.
Benoit Mandelbrot, who coined the term ‘fractal’ in 1975, described it as a ‘rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced size copy of the whole”, supplemented his definition with breath-taking computer visualizations. Gaston Julia, whose is known for another well-known fractal, Julia set, took pain in drawing that fractal in 1920s, but barely be a match to what Mandelbrot achieved with the modern computer graphics in 1970s.
Common features of fractals include having a simple and recursive definition, possessing a property called self-similarity and having fine structure at arbitrarily small scales.
Mandelbrot set is a prime example of mathematical visualization, which arises out of a simple definition of a complex quadratic polynomial, zn+1= zn2 + c, when considered with some conditions. Julia set was later discovered to be a special case of Mandelbrot set.
In nature, fractal properties are exhibited by clouds, mountain ranges and partly by coastlines, to name a few. In art, Jackson Pollock, whose painting No.5, 1948 is the costliest painting in the world sold for $142.7m, employed fractal patterns in his work.
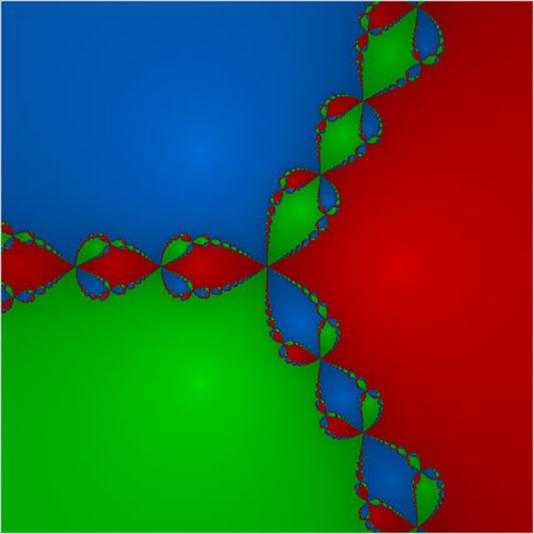
Many of us know about Newton Raphson’s Method, a potent algorithm for finding roots in complex plane. The questions that used to bother us happened to have only 2 roots, so the method would give us the nearest root. How about applying Newton Raphson’s Method to equations having 3 roots? Which root will it give? These questions encountered by John Hubbard, Cornell University Professor, convinced him to look for computer simulation to this confusing question. Experiment included running the algorithm and as Steven Strogatz said in his NYT column, telling it “to color-code millions of different starting points according to which root they approached, and to shade them according to how fast they got there”. Result? A marvelous fractal was discovered by him in which a third color would push itself in between the other two roots. The emerging root was very tough to decide as it happens with any chance game.
After Bednorz and Mueller research about superconductivity, for which they were awarded the Noble Prize, all the others’ research has been fruitless in giving any theories explaining Superconductivity. But if the fractals prove to be the game-changer, surely a break-through might be around the corner.
For the more concerned
Fractals Generators
- Chaospro is a free 2D/3D fractal generator available at www.chaospro.de
- Fractint is another generator which can be downloaded from www.spanky.triumf.ca/www/fracint/fractint.html
Tutorials
–Wikipedia article on Fractal and Mandelbrot Set (Disclaimer: Contains mathematical jargon)
-Yale University introductory course on fractals at www.classes.yale.edu/fractals
– www.fractalarts.com contains very good links, tutorials.
-Fractals at open directory project at www.dmoz.org/science/Math/Chaos_And_Fractals
